Os conceitos da geometria plana têm grande incidência no Enem, com recorrência de questões que exigem o conceito de área ou até mesmo noções básicas de ângulos. Além disso, ela é base para a geometria espacial, porém, a diferença entre ambas é que a primeira é bidimensional, e a segunda, tridimensional.
Conceitos da geometria plana
A construção da geometria plana, conhecida também como geometria euclidiana, deve-se aos conceitos básicos de ponto, reta e plano e às construções realizadas com base nesses elementos primitivos. Vale ressaltar que não existe definição para ponto, reta e plano, e, por isso, são conhecidos como elementos primitivos, porém todos nós conhecemos esses elementos de forma intuitiva.
→ Pontos: são sempre representados por letras maiúsculas do nosso alfabeto.
→ Retas: são sempre representadas por letras minúsculas do nosso alfabeto.
Com base na ideia que temos de reta, lembrando que ela é ilimitada, ou seja, infinita para os dois lados, surgem os conceitos de semirreta e segmento de reta. A fim de compreender melhor esse elemento essencial para a geometria.
→ Semirreta: é parte de uma reta que possui início, mas não possui fim.
→ Segmento de reta: é um segmento que se encontra entre dois pontos, ou seja, é limitado tanto no começo quanto no final.
→ Plano: é representado pelas letras do alfabeto grego.

Para aprofundar-se mais nesses conceitos fundamentais para essa área da matemática, leia o texto: Noções primitivas de geometria: ponto, reta, plano e espaço.
Posição relativa entre ponto e reta
Conhecendo os elementos primitivos, é possível fazermos análise da posição relativa entre ponto e reta.
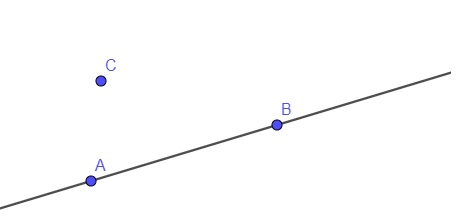
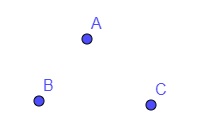
Note que os pontos A e B pertencem à reta r → dizemos que ; A ∈ r; B ∈ r.;
E que o ponto C não pertence à reta r → dizemos que C ∉ r.
Posição relativa entre duas retas
Duas retas podem ser paralelas, concorrentes ou coincidentes.
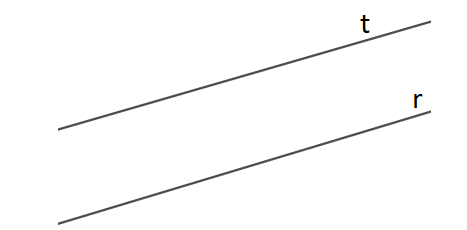
→ Retas paralelas: quando não possuem nenhum ponto em comum. A representação delas é feita com duas barras c // b (lê-se: c paralela a b).
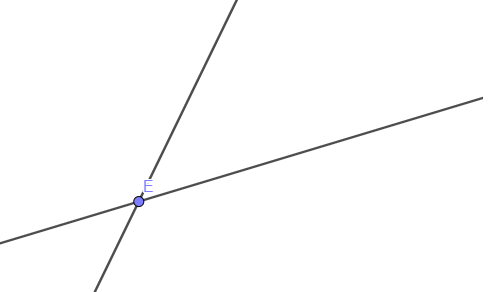
→ Retas concorrentes: quando possuem um único ponto em comum.
→ Retas coincidentes: quando possuem infinitos pontos em comum, ou seja, elas são iguais.
Para saber mais sobre esse tipo de posição.
Ângulos
Outro conceito muito importante é o de ângulo, que é a região formada pelo encontro entre duas semirretas. O ângulo é medido em graus e é classificado de acordo com a sua medida.
→ Ângulo agudo: menor que 90º
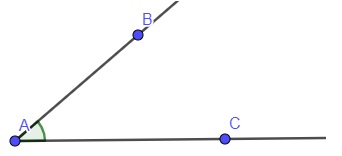
→ Ângulo reto: mede exatamente 90º.
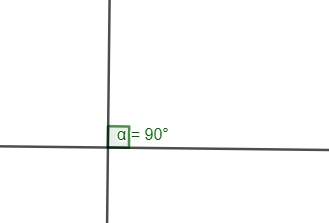
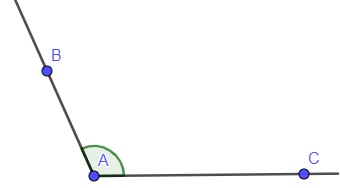
→ Ângulo obtuso: maior que 90º
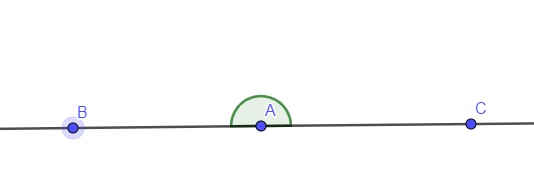
→ Ângulo raso: mede exatamente 180º.
Figuras planas
Definimos como figura plana qualquer representação fechada feita no plano, porém existem casos especiais, conhecidos como polígonos, além da circunferência, que possuem propriedades e fórmulas que dependem da sua forma.
Polígonos
Dentro das figuras planas, há várias figuras geometricas, algumas são mais conhecidas, como os quadriláteros, os triângulos, os pentagonos e os hexagonos. Quando a figura é fechada por segmentos de reta formando ângulos, ela é conhecida como polígono, logo, a união de segmentos de reta fechados forma as principais figuras planas, conhecidas como polígonos.
Eles são nomeados de acordo com a quantidade de ângulos ou mesmo de lados que possuem, por exemplo, triângulo (três ângulos), quadrilátero (quatro lados), pentagono (cinco ângulos). Os poligonos mais comuns são os triângulos e os quadriláteros (quadrádo, retângulo, losango e trapézio).
Os principais cálculos envolvendo os polígonos é o de perímetro, que nada mais é que a soma de todos os lados da figura, e o de área, que depende da sua forma, ou seja, cada figura terá uma fórmula para esse cálculo.
→ Área de triângulos
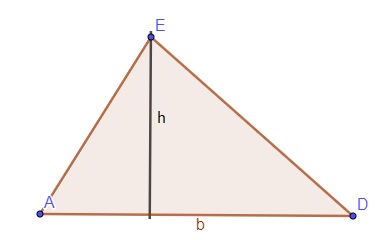
![]()
b: base
h: altura
→ Área de quadriláteros
Área de um quadrado

A = l²
Área de um paralelogramo

A = b . h
Área de um retângulo
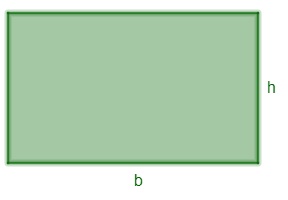
A = b . h
Área de um losango
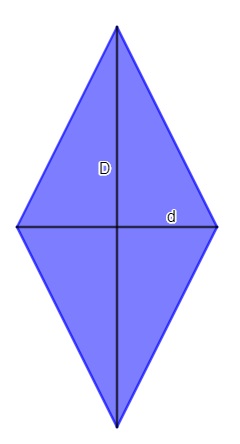
![]()
D: diagonal maior
d: diagonal menor
Área de um trapézio
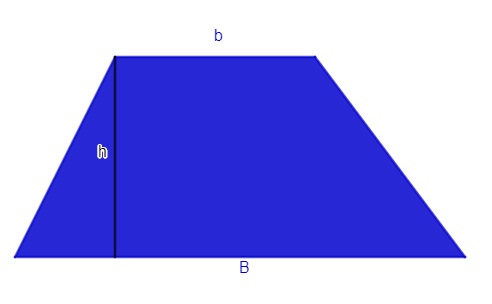
![]()
B: base maior
b: base menor
Círculo e circunferência
O círculo não é considerado um polígono, afinal ele não possui lados, mas é uma figura plana de grande importância. Nele calculamos o que chamamos de comprimento de circunferência (C), que é análogo à ideia de perímetro, ou seja, o comprimento do contorno. Também é possível calcular a área.
Chamamos de circunferência o contorno e de círculo toda a região desde o centro até o contorno.
Área de círculo e comprimento de circunferência
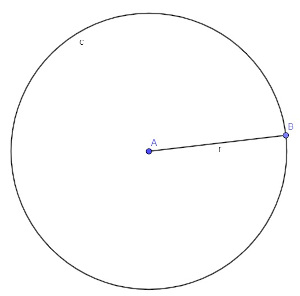
C = 2πr
A = πr2
r: raio da circunferência
Geometria plana no Enem
Na prova do Enem, as questões que envolvem a geometria plana, em sua maioria, são médias ou médias fáceis. Elas costumam combinar-se com outros conteúdos, por exemplo, noções de escala e proporção.
O conteúdo mais cobrado da geometria plana no Enem é, sem dúvida, a noção de área de polígonos e de circunferência, além dos estudos específicos para triângulos. Vale ressaltar que até mesmo questões sobre trigonometria e geometria espacial exigem que o candidato domine a geometria plana.
Analisando os cadernos amarelos de 2014 até 2019, existe uma variação na quantidade de questões de geometria plana, não obstante, pode-se afirmar que são, no mínimo, cinco questões por ano.
→ 2019
139 - Noções básicas da geometria plana
149 - Círculo e circunferência
151, 169 - Área
171, 175 - Triângulos
→ 2018
139, 169 - Noções básicas de geometria plana
142 - Área
155 - Ângulos
→ 2017
137, 169 - Áreas
147 - Noções básicas de ângulo
157 - Círculo e circunferência
175 - Círculo, circunferência e triângulo equilátero
→ 2016
154, 159, 166, 175 - Área de figuras planas
179 - Conceitos básicos da geometria
171 - Círculo e circunferência
→ 2015
143, 151, 161, 171 - Área de figuras planas
140 - Triângulo equilátero e círculo
148 - Noções básicas da geometria plana
→ 2014
136, 154 - Noções básicas da geometria plana
159 - Área
163, 168 e 174 - Retângulos
166 - Triângulos

Comentários
Postar um comentário